- 月赛题解
【202508】月赛语法组题解
- @ 2025-8-6 11:12:11
语法组月赛视频讲解
▶ 点击查看讲解视频
T1
思路
矩形面积
半圆面积
T2
思路
根据题目意思,可以知道,我们要求的两位数要尽可能的小,一位数尽可能的大。这样才能够保证差值最小。
对三个数字进行从小到大排序,因为题目要求两位数的十位不能为 ,所以要进行特殊判断。如果有一个 ,就需要放到两位数的个位,如果有两个 ,就需要保证两位数的十位为非 的数字。
T3
思路
题目要求插入数字之后的最大值,所以我们尽可能的靠前插入,在插入的时候满足 当下遍历的数字即可。
如果发现都没有可插入的位置,就把 放在数字串最后即可。
T4
思路1:桶排序
- 桶计数法:我们可以使用两个桶(数组)来记录比赛需要的难度值和已准备的难度值的出现次数。
- 比较两个桶:对于每一个比赛需要的难度值,检查已准备的题目中是否包含该难度。如果没有包含,则需要新增该题目。
- 统计结果:统计所有未被覆盖的难度值的数量,即为需要新增的题目数量。
思路2:双指针
-
双指针遍历:由于 数组是严格递增的, 数组是非递减的,可以利用双指针技术高效地检查 中是否包含 中的每个元素。
- 初始化两个指针
i和j,分别指向 和 的起始位置。 - 对于每个 ,在 中寻找是否存在 。如果存在,则不需要新增题目;否则需要新增一道题目。
- 由于 是非递减的,可以跳过比当前 小的 值。
- 初始化两个指针
-
贪心匹配:通过双指针的贪心匹配,可以确保每个 最多被检查一次,从而将时间复杂度优化到 。
T5
思路
-
的情况:
- 当 时,生成的数字 可以表示为 重复 次。例如,, 时,。
- 这种数字一定可以被 和另一个由 重复 次组成的数(如 , , ..., 即 $\frac{10^{k \cdot \text{len}(x)} - 1}{10^{\text{len}(x)} - 1}$)整除,因此 是合数。
- 结论:只要 , 一定是合数,直接输出
NO。
-
的情况:
- 此时 ,只需判断 本身是否为质数。
- 需要单独处理 的情况( 不是质数)。
- 对于其他 ,判断是否为质数即可。
T6
思路
-
时
- 根据贪心思路,易得将 数组排序后两两对齐配对的结果最优。
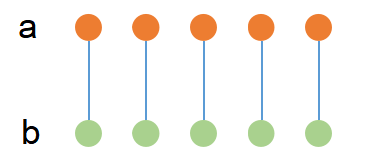
- 根据贪心思路,易得将 数组排序后两两对齐配对的结果最优。
-
时
- 有一次免费机会,选择 与 中的任意一个都有可能,需要枚举选择最优。枚举免费机会 , 与 中剩余部分依旧是两两对齐配对,计算当前方案 ,整体为
- 之前免费方案为 与 ,其代价为 , 现在免费方案为 与 ,其代价为 。观察可以发现:
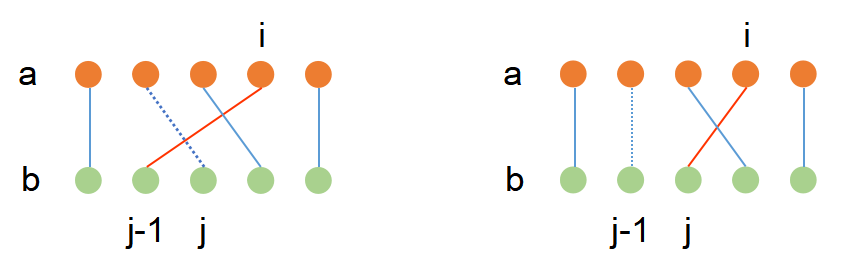
- 之前免费方案为 与 ,其代价为 , 现在免费方案为 与 ,其代价为 。观察可以发现:
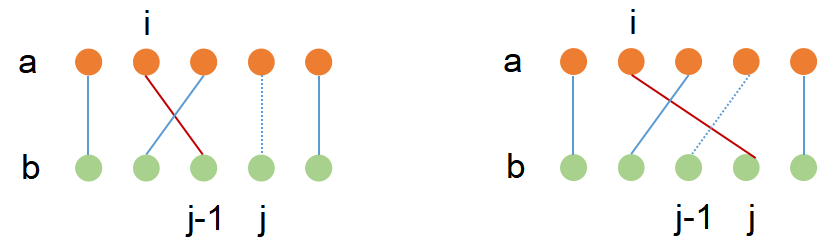
与上第一个规律类似,提前预处理出 与 进行免费配对后的代价,再使用以上规律计算即可,可将最内层优化至 ,总复杂度
0 条评论
目前还没有评论...
